Normal Distribution Curve: What Is It And Why It’s Used

Normal Distribution Curve: What Is It And Why It’s Used By The Six Sigma Approach

Six Sigma is a methodology dependent on the analysis of data to assist with problem-solving. Several mathematical and statistical principles, including the normal distribution curve, are used in this approach. The core statistical principles required to fix problems using Six Sigma rules are covered in many Lean Six Sigma courses. As it is usually briefly mentioned in online Six Sigma programs, Six Sigma concepts rely significantly on a grasp of the normal distribution curve. This article will cover what a normal distribution curve is, and how to use it.

What Is The Bell Curve, Or Normal Distribution Curve?

The normal distribution curve, also referred to as the Gaussian Distribution (Gaussian Curve) or bell-shaped curve, is the name used to define the mathematical idea that refers to the curve that is formed when a sequence is planned by using the data facts for a thing that meets the standards of “Normal Distribution.”

Where Can We Find A Normal Distribution Curve?

You can find representations of a normal distribution curve in several natural occurrences. For example, if you were to take note of all heights of men all around the world, what you find will show a consistent bell-shaped pattern. This trend is also observed in climate. The measurements would be following a bell curve shape if you measured the median midday temperature for June days in the United States every year. You may also get an average normal distribution curve by measuring the height among all your coworkers, or even the time it takes them to finish a glass of water.

What Are The Mean, Median And Mode Of A Normal Distribution Curve, And How Do You Calculate Them?

Now, let’s get into the basics of how a normal distribution curve is constructed. The value near the center is the peak on the arc of the line, since it contains the worth of the largest number of data points. The mean, meaning the average of a normal distribution curve, would be this point. If we continue with the height example,  you can say that there could be a higher number of men that are of average height than just about any other height, hence the global average height of men will be located at the peak of the normal distribution curve.

Keep in mind that in the event of normally distributed information, the mean is the same as the median, and mode. Let’s look at what the median, mean and mode are and how they differ.

When it comes to the Normal Distribution Curve, the mean is equal to the sum of all of the data points’ values, split by the total number of data points. The median is the midway value when all values are ordered from least to greatest. The mode, on the other hand, is defined to be the number that appears the most frequently in a group of data points. In conclusion, the mode, median and mean will all be the same in a normal distribution.

Outliers And The Normal Distribution Curve

The middle of the normal distribution curve is dense, and it declines on each side. This is notable because, when comparing it to other distributions, all of the data exhibits fewer outliers or specific causes of variation. The curve smooths thanks to the fact that the dataset includes few severe numbers on both the high or low end of the curve. The appearance of a bell of the normal distribution curve is due to this.

Standard Deviations In The Normal Distribution Curve

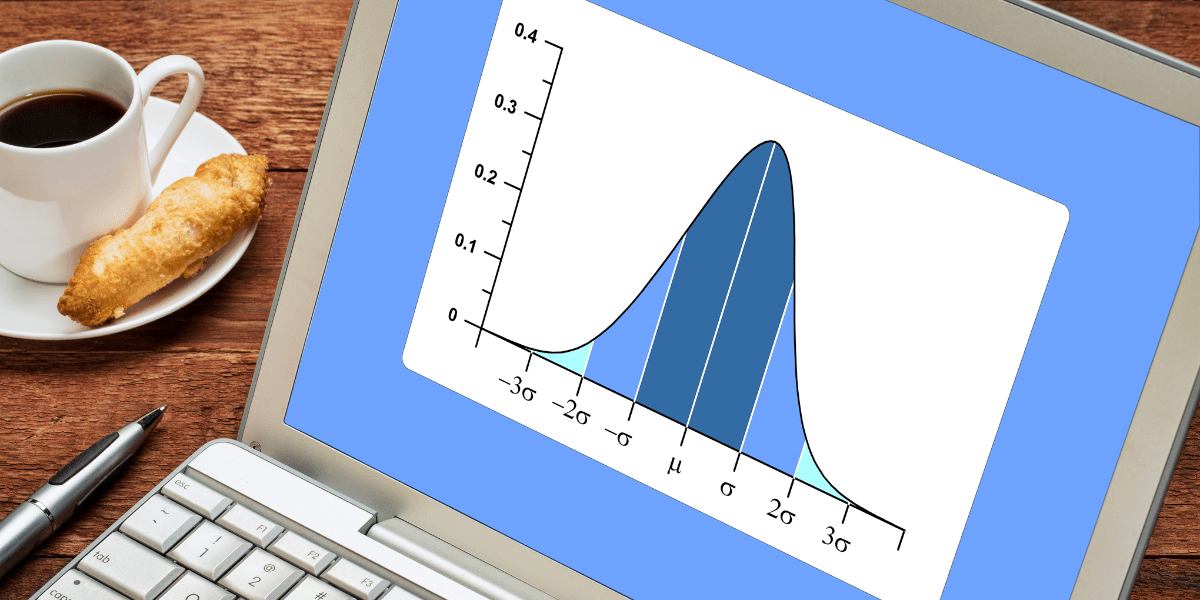
To understand this, let’s try to see a normal distribution curve from a different perspective. We know the mean and standard deviation are very important parameters in a curve graph, so first, let’s go through the meaning of standard deviation. The term standard deviation refers to a measure of exactly how tightly or broadly a collection of data seems to be clustered. This is among the measures of dispersion. The mean of a typical normal distribution is 0, while the standard deviation is 1. The mean decides the center’s location, while the standard deviation defines the bell’s width and height.

A big standard deviation, for instance, produces a smooth and broad bell, whereas a smaller standard deviation produces a steep and narrow curve. The rule is straightforward. The bigger a variation is, the flatter of a curve you will get. If you have a steeper of a curve, it is only logical to get a lower variation.

A Simple Example Of A Normal Distribution Curve

When you throw just one die, the probability of every number being rolled would be an approximate 16.67 percent.  If you throw two of them, it will range from two to twelve, respectively.  However, the biggest likelihood is to have the result as seven, which is really 2 + 12 / 2.

What is total number of dots is going to be if you throw all three dice at the very same time. The outcome will range from three to eighteen. However, as you can see, the likelihood of reaching a total of ten or eleven will be the highest, which would be close to ten and a half when determined by multiplying three plus eighteen by two.

According to the empirical standard deviation rule, a standard normal distribution should follow these concepts:

• Within 1 standard deviation of the mean, 68 percent of the data points will fall.
• Within 2 standard deviations, 95 percent of the data points will fall.
• Within 3 standard deviations of the mean, 99.73 percent of the data points will fall.

What We Have Learned

To wrap things up, let’s summarize what we have learned. The normal distribution curve is the name for a probability distribution in which the most common value is in the center and the other probabilities proportionally fall in both sides. It does not, in theory, approach zero.  With equal values lying on each side of the most often occurring value, a normal distribution curve could be split in half. It also shows us  a chance or arbitrary variation.  The process’s center is represented by the top of a normal distribution curve. Lastly, a normal distribution curve is separated into three standard deviations, each of them on a side of the mean.

If we’re talking about essential statistical concepts in regards to Lean Six Sigma, the normal distribution curve is definitely one of them. When the number of faults is excessively large, Lean Six Sigma is used to tackle the problem. A large number of faults statistically equates to a high level of process variation. Using the normal distribution curve, you can depict any dataset’s variation. The information shown by the curve may be production interruption or even the time required for a help desk line to take a phone call. If the information and data flows in a normal distribution curve, it is suitable for specific statistical tests employed in the Six Sigma analyze phase.

Did you know you that you can earn a project management certification WITHOUT any work experience?  It’s called the Certified Associate in Project Management or CAPM and it’s a great stepping stone into the lucrative field of project management.  It’s as easy as taking a CAPM Exam Prep course and applying to take the exam.  Some CAPM Exam Prep courses (like this one) even include a 100% pass guarantee and give you the 23 education hours required to take the exam.

Check out the article A Simple Guide to CAPM Certification

You might also be interested in our article on the Best online CAPM exam preparation tips